Les 8 idees estadístiques més importants: bootstrapping i la inferència basada en la simulació
Aquest article és el segon d’una sèrie d’entrades on exploro les 8 idees estadístiques més importants dels últims 50 anys, segons la revisió de Gelman i Vehtari (2021). Et convido que m’acompanyis en aquest camí d’aprenentatge mentre aprofundim en el tema d’avui: bootstrapping i la inferència basada en la simulació.
Introducció a la sèrie: Les 8 idees estadístiques més importants
Els últims cinquanta anys han vist avenços significatius en el camp de l'estadística, canviant la manera d'entendre i analitzar dades. Gelman i Vehtari (2021) han revisat les 8 idees més importants en estadística dels últims 50 anys.
Com a part del meu camí d'aprenentatge, he decidit aprofundir en aquestes 8 idees i compartir els meus descobriments. A cada article trobaràs una introducció a un concepte, així com alguns recursos per aprendre'n més. Així que, si t'interessa l'estadística, ets al lloc adequat!
Com obtenir dades de tot el món i no morir en l’intent
Posa’t en situació: estàs sopant amb nou amics i algú té la brillant idea de comparar els temps d’ús del mòbil. Cadascú treu el seu telèfon i comparteix quantes hores al dia dedica a la pantalla. Hi ha sorpreses i riures.
Algú pregunta: «quina deu ser la mitjana de temps d’ús al món?». Un amic diu que és una pregunta estúpida: «podem calcular la nostra mitjana, però la de tot el món? Impossible». Algú més optimista suggereix: «potser podríem extrapolar a partir de les nostres dades».
Aquest és un problema estadístic freqüent: tenim una mostra de dades i volem estimar la distribució en una població.
La població és una idea abstracta: representa a tots els subjectes d’interès. En el nostre cas, tot el món. En altres casos —més realistes— podria tractar-se de tots els estudiants d’un país, tots els ossos d’una muntanya específica o tots els ceps d’un vinyar.
Abans de seguir, aturem-nos a pensar: què és una mostra?
D’on surten les mostres? Gashapon!
Et sona aquesta màquina?
És un tipus de màquina expenedora anomenada gashapon al Japó. Insereixes monedes, gires la roda i obtens quelcom1 a l’atzar.
Imagina un gashapon gegant amb vuit mil milions de càpsules. Cada boleta representa a una persona al món i conté un número: el temps d’ús d’aquella persona. Totes aquestes càpsules són la població.
En compartir els temps d’ús al sopar estàvem, d’alguna manera, agafant deu càpsules d’aquesta màquina. Els números que vam obtenir són la nostra mostra.
Inferència estadística
Tenim una mostra. I ara què? Necessitarem la inferència estadística: un conjunt d’eines per deduir característiques de la població a partir d’una mostra.
Tradicionalment, abans de fer qualsevol càlcul, necessitaríem assumir una distribució (forma) particular en la població. Normalment s’assumeix una «distribució normal»:
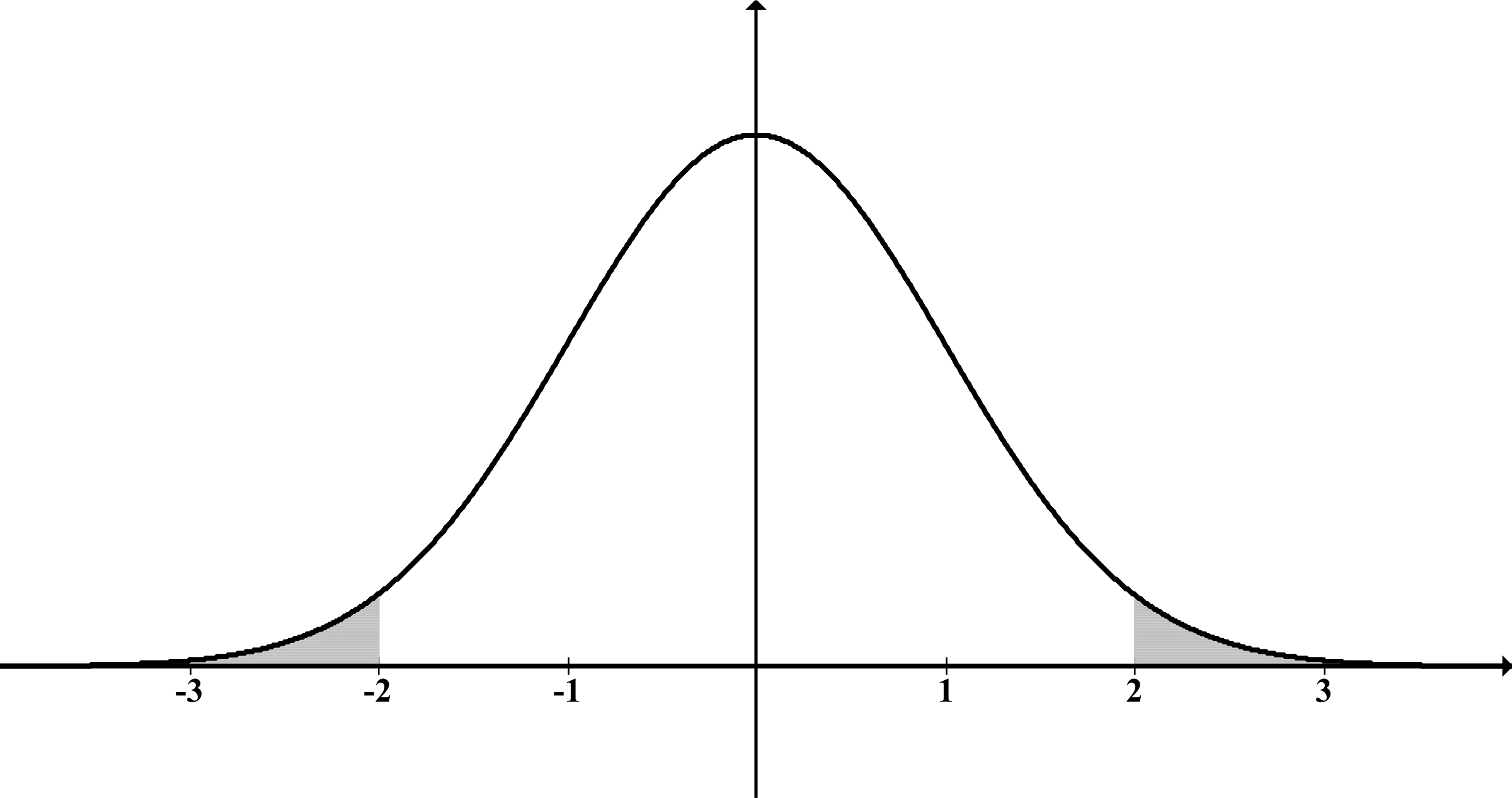
Com pots veure, és simètrica respecte a la mitjana (el punt més alt del gràfic), per tant, hi ha la mateixa quantitat de valors per sobre com per sota d’aquesta.
Però, i si el temps d’ús és asimètric? Tenint en compte que aproximadament el 15% de la població no té telèfon intel·ligent, és molt possible que sigui així.
Hi ha vegades que no podem o no volem assumir una distribució particular per a la població. Afortunadament, hi ha una alternativa per aquestes situacions.
Inferència basada en la simulació
La inferència basada en la simulació utilitza mostres simulades per fer prediccions a partir d’una sola mostra. Alguns exemples d’aquest enfocament són el bootstrapping, mètodes de Monte Carlo basats en cadenes de Markov, la prova de permutació i la calibració basada en la simulació.
Explorem el que es podria considerar com l’exemple més pur d’inferència basada en la simulació: el bootstrapping.
Bootstrapping: Gashapon Remix
Recordes el gashapon gegant amb vuit mil milions de càpsules? D’allà vam treure (metafòricament) les deu xifres de la mostra original del sopar. Posem aquestes càpsules en un nou gashapon de mida normal.
El nou gashapon té la mostra original i una nova funció: un botó de barreja aleatòria.
Farem servir aquesta màquina per generar la nostra primera mostra bootstrap. Necessitarem:
- Agafar una càpsula i anotar el número.
- Tornar la càpsula a la màquina i prémer el botó de barreja.
- Repetir els passos 1 i 2 fins que hàgim anotat deu números.
Això és tot! Els deu números que hem anotat són la nostra mostra bootstrap. Fàcil, oi?
Fixa’t que aquesta vegada tornem a posar la càpsula a la màquina. Això s’anomena mostreig amb reemplaçament. Implica que pot sortir el mateix número més d’una vegada. A més, com que les estem barrejant, totes les càpsules tenen la mateixa probabilitat de ser triades, cada vegada. Això fa que cada tria sigui independent, com si estiguéssim fent servir la màquina de vuit mil milions de boletes.
Però… per què?
La idea clau (i el supòsit principal) és que considerem que la nostra mostra original és una aproximació raonable de la població. Per tant, les mostres bootstrap reflecteixen la variabilitat i característiques de la població.
En una paraula: generar mostres bootstrap ≈ mostrejar de la població.
Com pots imaginar, una sola mostra bootstrap no és massa útil. Normalment necessitem entre 50 i 10.000. Per repetir el procés tantes vegades fem servir ordinadors.
Prova-ho!
He construït un petit simulador de gashapon basat en el nostre exemple. A la primera fila veuràs la nostra mostra original: el temps d’ús de cada amic.
Quan prems el botó «Crea una mostra bootstrap», el teu dispositiu seguirà els passos 1 a 3 de l’apartat anterior i et mostrarà les deu càpsules triades.
Veuràs que cada mostra bootstrap és única: una càpsula pot aparèixer més d’una vegada —o cap— i cada mostra té una mitjana diferent.
Mostra original • Mitjana = ? hores
Última mostra bootstrap • Mitjana = ? hores
Histograma de mitjanes bootstrap
Interval de confiança del 95%: ?-?
L’histograma anterior mostra una barra per a cada mitjana que has generat. La seva alçada és proporcional al nombre de vegades que ha aparegut. Pots interactuar amb les barres per veure la mitjana i freqüència que representen.
T’ha sortit una barra ? Aquesta és la mitjana de la mostra original. Era la més alta al teu experiment? No sempre ho és.
Sota l’histograma pots trobar algunes estadístiques sobre les mitjanes bootstrap, incloent-hi l’interval de confiança del 95%. Aquest és el rang de valors on esperaríem trobar la mitjana de la població. Amb els teus resultats, conclouríem que la mitjana de temps d’ús del món es troba entre ? i ? hores.
T’has fixat en com canviava l’interval de confiança a mesura que generaves més mostres? Com més mostres tinguem, més estable es torna.
Cada vegada que cliques «Reset», la mostra original canvia. Necessitaràs una mica de sort per provar això, però mira què passa quan els valors originals són asimètrics (per exemple, la majoria dels valors estan per sota de la mitjana). Com afecta això a la forma de l’histograma?
No és màgia — limitacions
Potser has pensat: «i si tots els nostres amics odien els mòbils i tenen zero hores d’ús (o potser estan enganxats)? No estaríem assumint que tot el món és així?». Tens tota la raó; aquesta és una de les limitacions de la inferència basada en la simulació. En resum: com que tractem la mostra original com si fos la població, val més que aquesta sigui representativa. Si està esbiaixada, el nostre interval de confiança i conclusions també ho estaran.
L’altra gran limitació explica els resultats possiblement decebedors: «la mitjana de temps d’ús global està entre 5 i 12 hores? Una mica imprecís, no?». Sens dubte. Aconseguir una estimació precisa d’una mostra tan petita estaria més a prop de la màgia que no pas de l’estadística.
Com més gran sigui la nostra mostra original, més estret serà l’interval de confiança. Si tinguéssim el 100% de les dades de la població, l’interval seria només una xifra: la mitjana real de la població (per exemple, 4-4). Com menys dades tinguem, menys confiança tindrem en els valors predits, resultant en intervals més amplis.
Conclusió
En aquest article hem après sobre la inferència basada en la simulació mitjançant el bootstrapping.
El bootstrapping ens permet estimar gairebé qualsevol distribució sense necessitat de recol·lectar més mostres de la població i sense fer suposicions sobre la distribució de les dades, a diferència dels mètodes estadístics tradicionals.
Un gran avantatge del bootstrapping és que es pot aplicar a gairebé qualsevol situació sense equacions matemàtiques complicades. Tot i això, és important recordar les dues limitacions principals: la mida de la mostra i la seva representativitat.
Un altre punt fort d’aquesta tècnica és que no es limita a les mitjanes; el bootstrapping és simplement el procés de generar les mostres sintètiques. Per tant, podem fer servir les mostres bootstrap per calcular la mediana, moda, desviació estàndard, correlació, coeficients de fiabilitat o fins i tot la grandària de l’efecte2.
Força potent, no creus?
En el pròxim article de la sèrie aprendrem sobre els models sobreparametritzats i la regularització. Fins aviat!
Recursos d’aprenentatge
Video: Bootstrapping Main Idees!!! — StatQuest (2021). Josh Starmer té una molt bona introducció al bootstrapping al seu canal de YouTube StatQuest. Recomano molt aquest canal.
Article acadèmic: The frontier of simulation-based inference — Cranmer, Brehmer & Louppe (2020). Aquest article explora diferents mètodes d’inferència basada en la simulació, tot referenciant avenços recents en machine learning, i ofereix algunes recomanacions sobre quin enfocament triar.
No es tracta només de joguines; hi ha una mica de tot. He vist gashapon d’edificis, petites figures d’anime, models d’inodors japonesos (?), claus i botons d’engegar cotxes (??), i un de «gambes empanades i els seus amics» (part 2!!). Fa poc, un amic em va dir que va aconseguir un gashapon d’un gashapon. Meta.
La grandària de l’efecte és una mesura de la força d’un fenomen. En el context de la recerca, és el valor que quantifica l’efectivitat d’una intervenció (per exemple, una nova teràpia). Com que les grandàries de l’efecte són estimacions estadístiques, es recomana proporcionar intervals de confiança en comunicar-les. El bootstrapping seria una manera senzilla de calcular aquests intervals.