Las 8 ideas estadísticas más importantes: bootstrapping y la inferencia basada en la simulación
Este artículo es el segundo de una serie de entradas donde abordo las 8 ideas estadísticas más importantes de los últimos 50 años, según la revisión de Gelman y Vehtari (2021). Te invito a que me acompañes en este camino de aprendizaje mientras profundizamos en el tema de hoy: bootstrapping y la inferencia basada en la simulación.
Introducción a la serie: Las 8 ideas estadísticas más importantes
Los últimos 50 años han visto avances significativos en el campo de la estadística, moldeando la forma de entender y analizar datos. Gelman y Vehtari (2021) revisaron las 8 ideas más importantes en estadísticas de los últimos 50 años.
Como parte de mi camino de aprendizaje, he decidido profundizar en estas 8 ideas y compartir mis hallazgos. En cada artículo, encontrarás una introducción a un concepto, junto con algunos recursos de aprendizaje. Así que, si te interesa la estadística, ¡estás en el sitio correcto!
Cómo obtener datos del mundo entero sin morir en el intento
Ponte en situación: estás cenando con nueve amigos y alguien tiene la brillante idea de comparar los tiempos de uso del móvil. Cada uno saca su teléfono y comparte cuántas horas al día dedica a la pantalla. Hay sorpresas y risas.
Alguien pregunta: «¿cuál será el tiempo de uso promedio en el mundo?». Un amigo dice que es una pregunta estúpida: «podríamos calcular nuestro promedio, ¿pero el de todo el mundo? Imposible». Alguien más optimista sugiere: «quizás podríamos extrapolar a partir de nuestros datos».
Este es un problema estadístico habitual: tenemos una muestra de datos y queremos estimar la distribución en una población.
La población es una idea abstracta: representa a todos los sujetos de interés. En nuestro caso, todo el mundo. En otros casos —más realistas— podría tratarse de todos los estudiantes de un país, todos los osos en una montaña específica o todas las vides de un viñedo.
Antes de seguir, parémonos a pensar: ¿qué es una muestra?
¿De dónde salen las muestras? ¡Gashapon!
¿Te suena esta máquina?
Es un tipo de máquina expendedora llamada gashapon en Japón. Insertas monedas, giras la rueda y obtienes algo1 al azar.
Imagina un gashapon gigantesco con ocho mil millones de cápsulas. Cada bolita representa a una persona en el mundo y contiene un número: el tiempo de uso de esa persona. Todas esas cápsulas son la población.
Al compartir los tiempos de uso en la cena estábamos, de algún modo, cogiendo diez cápsulas de esta máquina. Los números que obtuvimos son nuestra muestra.
Inferencia estadística
Tenemos una muestra. ¿Y ahora qué? Necesitaremos la inferencia estadística: un conjunto de herramientas para deducir características de la población a partir de una muestra.
Tradicionalmente, antes de hacer cualquier cálculo, necesitaríamos asumir una distribución (forma) particular en la población. Normalmente se asume una «distribución normal»:
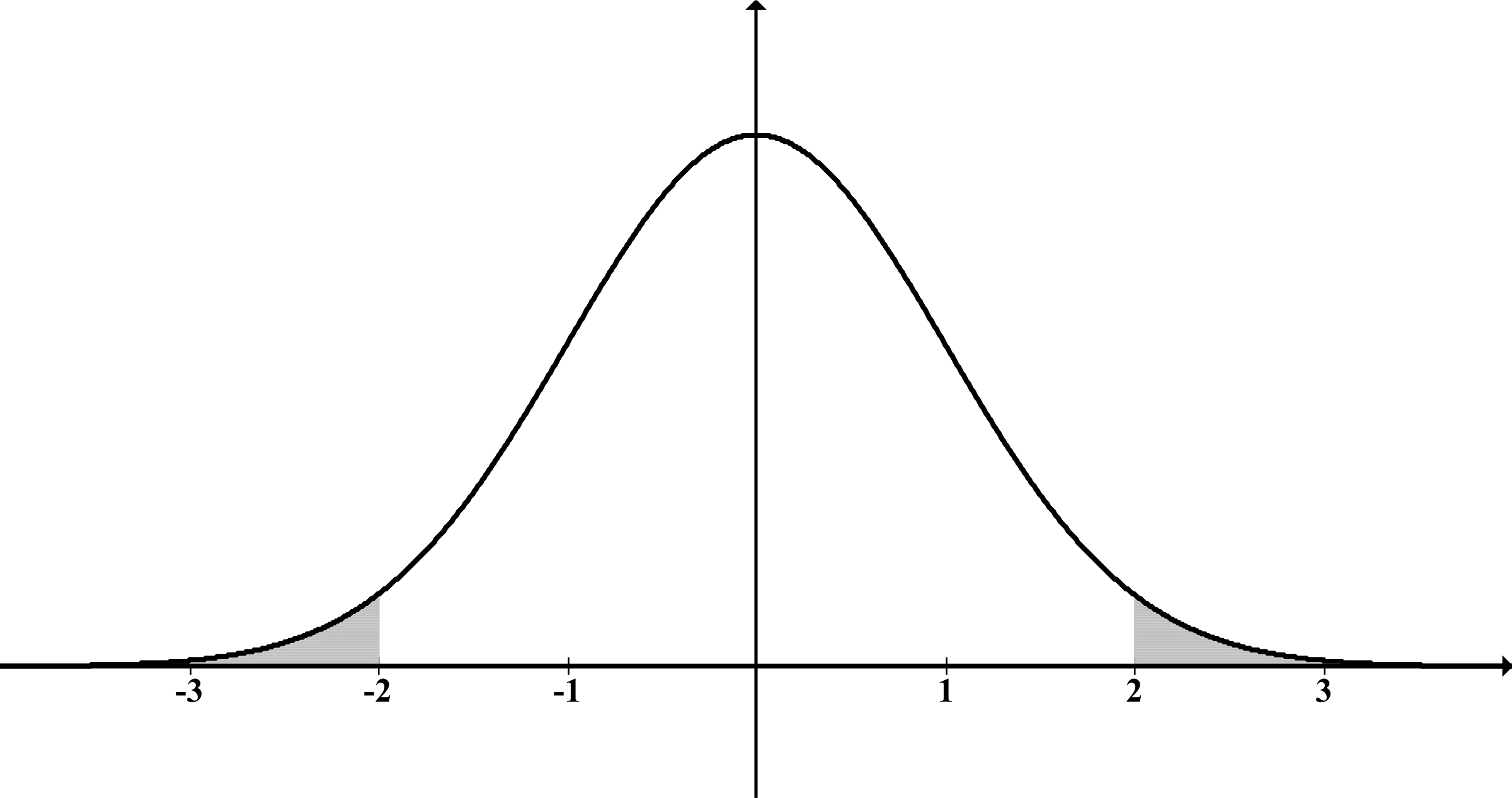
Como puedes ver, es simétrica respecto a la media (el punto más alto de la gráfica), por lo que hay la misma cantidad de valores por encima que por debajo de esta.
Pero, ¿y si el tiempo de uso es asimétrico? Teniendo en cuenta que el ~15% de la población no tiene smartphone, es muy posible que sea así.
Hay casos en los que no podemos o no queremos asumir una distribución particular para la población. Afortunadamente, hay una alternativa para estas situaciones.
Inferencia basada en la simulación
La inferencia basada en la simulación utiliza muestras simuladas para hacer predicciones a partir de una sola muestra. Algunos ejemplos de este enfoque son el bootstrapping, métodos de Monte Carlo basados en cadenas de Markov, la prueba de permutación y la calibración basada en la simulación.
Vamos a explorar lo que se podría considerar como el ejemplo más puro de inferencia basada en la simulación: el bootstrapping.
Bootstrapping: Gashapon Remix
¿Recuerdas el enorme gashapon con ocho mil millones de cápsulas? De ahí sacamos (metafóricamente) las diez cifras de la muestra original de la cena. Vamos a colocar esas cápsulas en un nuevo gashapon de tamaño normal.
El nuevo gashapon tiene nuestra muestra original y una nueva función: un botón de mezla aleatoria.
Usaremos esta máquina para generar nuestra primera muestra bootstrap. Necesitaremos:
- Tomar una cápsula y anotar el número.
- Devolver la cápsula a la máquina y pulsar el botón de mezcla.
- Repetir los pasos 1 y 2 hasta que hayamos anotado diez números.
¡Eso es todo! Los diez números que hemos anotado son nuestra muestra bootstrap. Fácil, ¿no?
Fíjate en que esta vez volvemos a poner la cápsula en la máquina. Esto se llama muestreo con reemplazo. Implica que puede salir el mismo número más de una vez. Además, como las estamos mezclando, todas las cápsulas tienen la misma probabilidad de ser elegidas, cada vez. Esto hace que cada toma sea independiente, como si estuviéramos usando la máquina de ocho mil millones de bolitas.
Pero… ¿por qué?
La idea clave (y el supuesto principal) es que consideramos que nuestra muestra original es una aproximación razonable de la población. Por lo tanto, las muestras bootstrap reflejan la variabilidad y características de la población.
En una palabra: generar muestras bootstrap ≈ muestrear de la población.
Como imaginarás, una sola muestra bootstrap no es demasiado útil. Normalmente necesitaremos entre 50 y 10.000. Para repetir el proceso tantas veces usamos ordenadores.
¡Pruébalo!
He construido un pequeño simulador de gashapon basado en nuestro ejemplo. En la primera fila verás nuestra muestra original: el tiempo de uso de cada amigo.
Cuando presiones el botón «Crear una muestra bootstrap», tu dispositivo seguirá los pasos 1 a 3 del apartado anterior y te mostrará las diez cápsulas elegidas.
Verás que cada muestra bootstrap es única: una cápsula puede aparecer más de una vez —o ninguna— y cada muestra tiene una media diferente.
Muestra original • Media = ? horas
Última muestra bootstrap • Media = ? horas
Histograma de medias bootstrap
Intervalo de confianza del 95%: ?-?
El histograma anterior muestra una barra para cada media que has generado. Su altura es proporcional al número de veces que ha aparecido esa media en particular. Puedes interactuar con las barras para ver la media y frecuencia que representan.
¿Te ha salido una barra ? Esa es la media de la muestra original. ¿Es la más alta en tu experimento? No siempre lo es.
Debajo del histograma puedes encontrar algunas estadísticas sobre las medias bootstrap, incluyendo el intervalo de confianza del 95%. Este es el rango de valores donde esperaríamos que esté la media de la población. Con tus resultados, concluiríamos que el tiempo de uso promedio global está entre ? y ? horas.
¿Has visto cómo cambiaba el intervalo de confianza a medida que generabas más muestras? A mayor número de muestras bootstrap, más estable se vuelve.
Cada vez que presionas «Reset», la muestra original cambia. Necesitarás algo de suerte para esto, pero prueba a ver qué ocurre cuando los valores originales son asimétricos (por ejemplo, la mayoría de los números están por debajo de la media). ¿Cómo afecta eso a la forma del histograma?
No es magia — limitaciones
Puede que hayas pensado algo como «¿y si todos nuestros amigos odian los móviles y tienen cero horas de tiempo de uso (o igual todos están enganchados)? ¿No estaríamos asumiendo que todo el mundo es así?». Tienes toda la razón; esta es una de las limitaciones de la inferencia basada en la simulación. En resumen: dado que tratamos la muestra original como si fuese la población, más nos vale que sea representativa. Si está sesgada, nuestro intervalo de confianza y conclusiones también lo estarán.
La otra gran limitación explica los resultados posiblemente decepcionantes: «¿el tiempo de uso promedio global está entre 5 y 12 horas? Un poco impreciso, ¿no?». Sin duda. Obtener una estimación precisa de una muestra tan pequeña estaría más cerca de la magia que de la estadística.
Cuanto mayor sea nuestra muestra original, más estrecho será el intervalo de confianza. Si tuviéramos el 100% de los datos de la población, el intervalo sería sólo un número: la media real de la población (por ejemplo, «4-4»). Cuanto menos datos tengamos, menos confianza tendremos en los valores predichos, resultando en intervalos más amplios.
Conclusión
En este artículo hemos aprendido sobre la inferencia basada en la simulación a través del bootstrapping.
El bootstrapping nos permite estimar casi cualquier distribución sin necesidad de recolectar más muestras de la población y sin hacer suposiciones sobre la distribución de los datos, a diferencia de los métodos estadísticos tradicionales.
Una gran ventaja del bootstrapping es que se puede aplicar en casi todas las situaciones sin ecuaciones matemáticas complicadas. Sin embargo, es importante recordar las dos principales limitaciones: el tamaño de la muestra y su representatividad.
Otro punto fuerte de esta técnica es que no se limita a las medias; el bootstrapping es simplemente el proceso de generar las muestras sintéticas. Por lo tanto, podemos usar las muestras bootstrap para calcular la mediana, moda, desviación estándar, correlación, coeficientes de fiabilidad o incluso el tamaño del efecto2.
Bastante potente, ¿no crees?
En la próxima entrega de la serie aprenderemos sobre los modelos sobreparametrizados y la regularización. ¡Hasta pronto!
Recursos de aprendizaje
Video: Bootstrapping Main Ideas!!! — StatQuest (2021). Josh Starmer tiene una muy buena introducción al bootstrapping en su canal de YouTube StatQuest. Recomiendo encarecidamente este canal.
Artículo académico: The frontier of simulation-based inference — Cranmer, Brehmer & Louppe (2020). Este artículo explora diferentes métodos de inferencia basada en la simulación, referenciando avances recientes en machine learning, y ofrece algunas recomendaciones sobre qué enfoque elegir.
No se trata sólo de juguetes; hay un poco de todo. He visto gashapon de edificios, pequeñas figuras de anime, modelos de inodoros japoneses (?), llaves y botones de encendido de coches (¿?), y uno de «gambas empanadas y sus amigos» (¡parte 2!). Hace poco, un amigo me dijo que consiguió un gashapon de un gashapon. Meta.
El tamaño del efecto es una medida de la fuerza de un fenómeno. En el contexto de la investigación, es el valor que cuantifica la efectividad de una intervención (por ejemplo, una nueva terapia). Dado que los tamaños de efecto son estimaciones estadísticas, es una buena idea proporcionar intervalos de confianza al comunicarlos. El bootstrapping sería una forma sencilla de calcular estos intervalos.